Set Theory
This page lists of the various symbols in the Set Theory group.
Symbols related to Set Theory
Symbols in this group:
Aleph-Null
Aleph-Null represents the infinite cardinality of the set of natural numbers.
Complement
The complement of a set A is the set that contains all elements that are not in set A.
Everything #2
Everything finite; the full set of definitive knowledge a system is capable of retrieving and ordering.
Intersection
The intersection of two sets is the set of objects that belong to both sets.
Natural Numbers Including Zero
Represents the set of all natural numbers including zero.
Natural Numbers Without 0
Represents the set that contains all the natural numbers except 0.
Nomega
Nomega is used for determining sets of numbers that include either a continuous and infinite set of positive numbers and zero OR a continuous and infinite set of negative numbers and zero.
Proper Subset (also called a strict subset)
A proper subset is subset that has few elements than the set, i.e., the subset can not be the original set.
Proper Superset (also called strict superset)
A proper superset is a superset that has more elements than a set.
Relative Complement
Refers to objects that belong to one set but are not in the other set.
set
A set is a collection of elements represented as a comma separated list of elements.
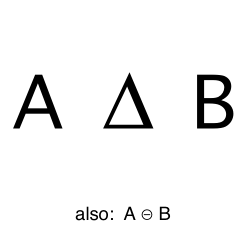
Symmetric Difference
Items that belong to two sets but not the intersection of the two sets.
Taurus
Taurus is the 2nd astrological sign in the zodiac, originating from the constellation of the Taurine.
Citation
Use the citation below to add this symbols group page to your bibliography:
Style:MLAChicagoAPA
"Set Theory Symbols." Symbols.com. STANDS4 LLC, 2025. Web. 26 Feb. 2025. <https://www.symbols.com/group/93/Set+Theory>.


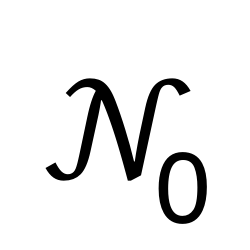
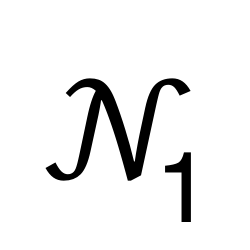




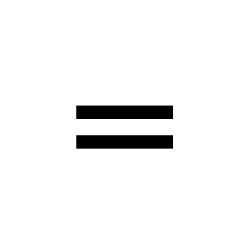



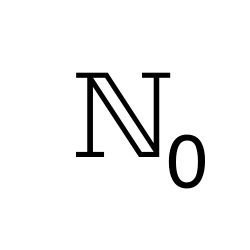
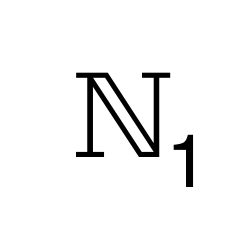
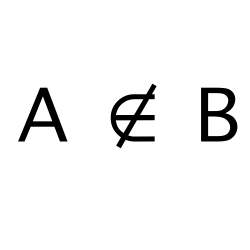
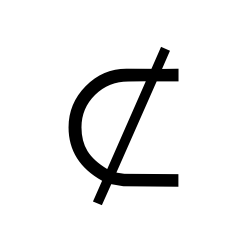

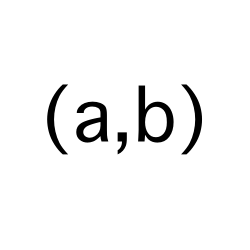
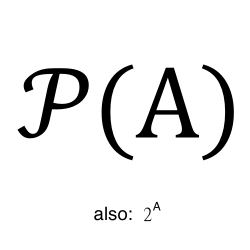




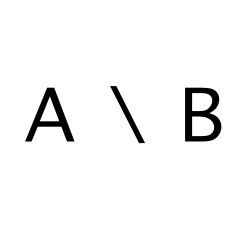


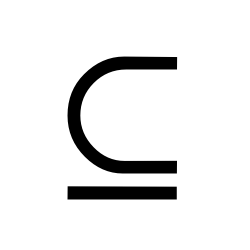
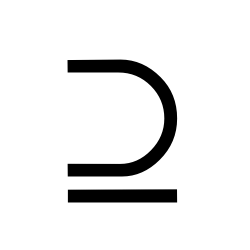







Have a discussion about the Set Theory group with the community:
Report Comment
We're doing our best to make sure our content is useful, accurate and safe.
If by any chance you spot an inappropriate comment while navigating through our website please use this form to let us know, and we'll take care of it shortly.
Attachment
You need to be logged in to favorite.
Log In